
今日は、早稲田実業中の今年の入試問題1⃣を解いていきましょう!!
2021年 早稲田実業中 1⃣(1)分数、小数の四則計算
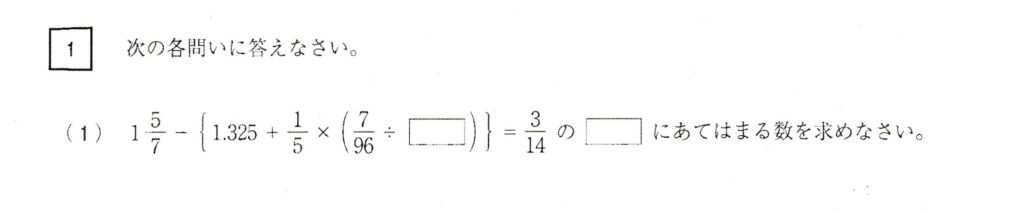
四則計算は、分数が含まれていて、テキストでは表示しにくいので、解法を画像で表示します。

解答2-1015x1024.jpg)
2021年 早稲田実業中 1⃣(2)比
問題-1024x124.jpg)
歯車A,B,Cの歯数の比を、下のように連比で求めます。
図-2-1024x450.jpg)
よって、Bの歯数:Cの歯数 = 20:24 = 5:6
ここで、歯車の歯数と回転数の関係は、
「Bの歯数×Bの回転数 = Cの歯数×Cの回転数」
であるから、この公式に、B、Cの歯数の比(5:6)と、Bの回転数72を代入すると、
5×72 = 6×□
360 = 6×□
□ = 360÷6 = 60
よって、歯車Cの回転数は、60回
2021年 早稲田実業中 1⃣(3)角度
問題-1024x537.jpg)
下図のように、比較的分かりやすい角度を書き出していくと、
辺ADと辺FCは平行で、錯覚が等しいので、∠ADF = ∠CFD = 24°
また、対角線ACは、正方形ABCDの∠C(90°)を二等分するから、∠DCG = ∠BCG = 45°
また、△DCGと△BCGは合同な三角形なので、下図のように、
∠CDG = ∠CBG(×) 、 ∠DGC = ∠BGC(〇)
となる。
図-1024x578.jpg)
∠CDG = ∠CBG(×)=∠D(90°)ー∠ADF(24°) = 66°
よって、△DGCの内角の和より、
∠DGC (〇)= 180°ー(45°+66°) = 180°ー111°= 69°
図より、∠(あ)= 180°ー(∠DGC + ∠BGC) = 180°ー69°×2
= 180°ー138°= 42°
2021年 早稲田実業中 1⃣(4)円錐、円柱の体積
問題-1024x492.jpg)
この影がつくる立体は下図の赤い部分になります。
分かりやすいように、元の円柱をABCDとし、底面の円の中心をO、電球をPとすると、点PからA、Dを通る延長線と、底面のBCの延長線の交わる点をE、Fとする。
平面図形のように説明していますが、実際は、点Pを頂点とし、半径OE(6cm)の円を底面、高さOP(4cm)の大きな円錐から、破線で示した小さな円錐(点Pを頂点とし、半径3cmの円を底面、高さ2cmの円錐)と元の円柱(半径3cm、高さ2cm)を除いた赤いスカートのような部分が、求める円柱の影の部分になる。
図-1024x561.jpg)
よって、大きな円錐ー(小さな円錐+円柱)
=(6×6×3.14×4÷3)ー(3×3×3.14×2÷3+3×3×3.14×2)
= 48×3.14ー(6×3.14+18×3.14)
= (48ー24)×3.14
= 24×3.14 = 75.36㎤
今日のまとめ
今日の問題の(1)と(3)は、多くの現小5の生徒さんが解けたことと思います。
(2)の問題では、歯車の歯数と回転数の関係を知らなければ難しいと思いますが、知っていれば、それほど難しくなかったと思います。
また、その前の連比の解き方もしっかりマスターしておいてくださいね。
(4)の影の問題は、図がイメージできるかどうかにかかっています。 図が分かれば、円錐の計算ミスにさえ気を付ければ、正解できる問題だと思います。







