今年のゴールデンウィークも今日で終わりですが、コロナのせいで、どこにも遊びにけず、ステイホームで、「GW(ガリ勉ウィーク)」だった受験生も多いのではないでしょうか?(;^_^A
しかし、その努力が来年春に実り、来年のゴールデンウィークは、志望校の1年生として、楽しく過ごせることを願っています!(^_^)
では、今日ゴールデンウィーク最終日は、女子御三家の一角であるJG女子学院中の入試問題1⃣(5)(6)、2⃣を解いていきましょう!!
2021年 女子学院中1⃣(5)整数問題、倍数算
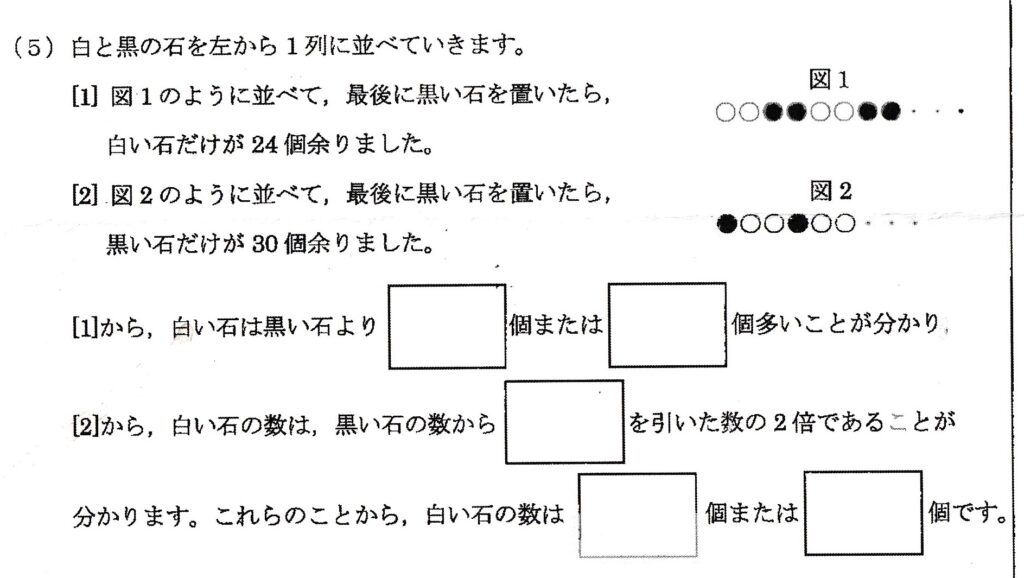
[1]より、〇〇●●」〇〇●●」〇〇●●」・・の並べ方で、最後に黒い石が2個置かれた状態「〇〇●●」の場合、並べられた白石と黒石は同じ数になるので、白石は、余った24個分だけ、黒石よりも多いことになる。
一方、最後に黒い石が1個置かれた状態「〇〇●」の場合、並んでいる白石と黒石では、白石が黒石よりも1個多い上に、24個余っているので、白石は、黒石よりも25個(1+24)多いことになる。
よって、最初の2つの□の答え:24個または25個多い
[2]より、●〇〇」●〇〇」●〇〇」・・の並べ方で、最後が「●〇〇」で終われば、並んでいる白石は、並んでいる黒石の2倍の数になる。・・①
ところが、問題文より、最後に黒石が置かれているので、
●〇〇」●〇〇」●〇〇」・・●〇〇」●
の並び方になる。
ここで、問題文より、白石は余りがないので、並んでいる白石の個数が、白石全部の個数となるが、黒石は、黒石全部の個数から、余った30個を引いた個数の黒石が並べられていることになる。・・②
ところで、①の考え方のように、●〇〇」の形で並び終えるようにするために、最後の黒石1個を取ると、余った黒石は、1個増えて31個となる。
●〇〇」●〇〇」●〇〇」・・●〇〇」● + 余り●30個
↓
●〇〇」●〇〇」●〇〇」・・●〇〇」 + 余り●31個・・③
よって、③の場合で考えると、①、②の考え方より、
「並んでいる黒石の個数 = 黒石全部の個数ー31個」
と考えられるので、
白石全部(並んでいる白石) = 並んでいる黒石×2
白石全部(並んでいる白石) = (黒石全部ー31個)×2
となる。
よって、3個目の□の答え:31
これらのことより、
(ⅰ)白石が黒石より24個多い場合
白石 = 黒石+24
と置き、
白石全部(並んでいる白石) = (黒石全部ー31個)×2
の式に代入すると、
黒石+24 = (黒石ー31個)×2
これを図で考えると、下の図のようになるので、

黒×2 ー 黒 = 24+62
黒 = 86個 となり、ここでは、白の個数を求めるので、
白石 = 黒石+24 = 86+24 = 110個
(ⅱ)白石が黒石より25個多い場合、(ⅰ)と同様にして、
白石 = 黒石+25
と置き、
白石全部(並んでいる白石) = (黒石全部ー31個)×2
の式に代入すると、
黒石+25 = (黒石ー31個)×2
これを図で考えると、下の図のようになるので、

黒×2 ー 黒 = 25+62
黒 = 87個となり、ここでは、白の個数を求めるので、
白石 = 黒石+25 = 87+25 = 112個
最後の2つの□の答え:110個または112個
2021年 女子学院中1⃣(6)面積、比
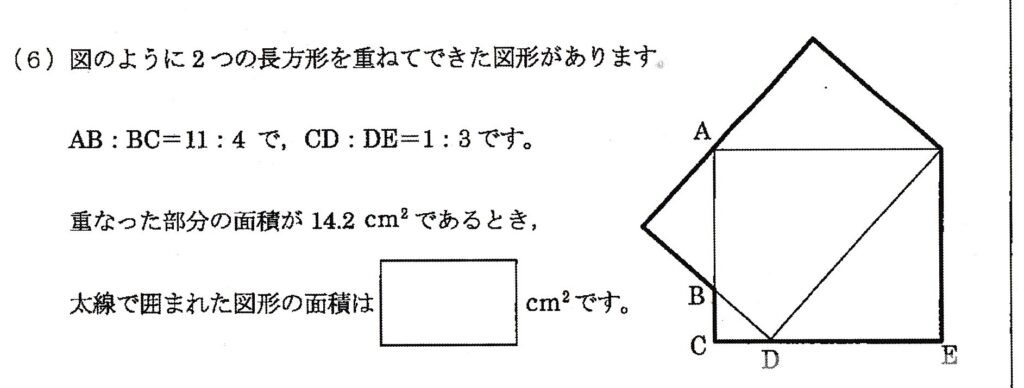
この問題は、テキストでは表示しにくいので、解法を画像で表示します。



2021年 女子学院中2⃣ 公倍数、公約数

(あ)と(い)の最大公約数が48ということは、(あ)と(い)は、48の倍数である。
そこで、48の倍数を書き出してみると、
48、96、144、192、240、288、336、384・・・
48の倍数同士を足して、和が384になるので、48~336の7個で考えればよく、その組み合わせは、
(あ、い)= (240、144)、(336、48)
の2組である。
*(あ、い)=(288、96)も和が384になるが、この2個の数字の最大公約数は96になるので、問題に合わない。
答え:240、336
今日のまとめ
今日の問題は、2⃣は簡単だったので、新小6の生徒さんはしっかり解いてほしいと思います。
1⃣(5)の問題は、「最後に黒石を置いたら」という表現から、解説のように「〇〇●●」という最後の並べ方と「〇〇●」という最後の並べ方の2パターン考えられるから、答えも2個考えられることに気づけるか、というか、答えが2個あるから、最後の並べ方が2パターンあるんだと気づいた受験生が多かったかもしれませんね。
1⃣(6)の辺の比と面積比の問題は、JGなど男女御三家を受験するレベルの生徒には、そこまで難しくはなかったと思いますが、標準的な新6年生レベルではまだ容易に解けないのではないかと思いますので、解説をしっかり読んで、マスターしてほしいと思います。
ちなみに、この問題の冒頭に「2つの長方形」とありますが、合同な長方形とは書いてありませんね。
しかし、解説文では、2つの長方形ACEFも長方形HDFGも面積は、同じ面積「△60」で表しています。
これは、解説では触れていませんが、△AFDを見ていただくと、△AFDは、長方形ACEFにとっても長方形HDFGにとっても、面積が1/2にあたるので、長方形ACEFも長方形HDFGも△AFDの2倍の面積になるということで、面積は等しいことになります。
Zoomを使った一対一オンライン授業のお知らせ
難関中学合格を目指し、当ブログをご覧いただいている読者のみなさま、いつもありがとうございます(^_^)
そんな読者の皆様に本日はお知らせがあります。
実は、3月1日から、web会議ツールのZoom(ズーム)を使って、読者の皆さまと中学受験算数の一対一のオンライン授業を始めたいと思っています。
いつも当ブログで解いているような難関中学校の入試問題レベルの難問でなくとも、塾や学校の宿題で分からない算数の問題を教えてほしいといった感じのことでもいいので、ご興味がある読者の方は、当ブログのプロフィールの下の「重吉へのメール」から、ご希望のメールをお送りください。
ちなみに、3月1日以降の月曜日から金曜日の朝10時から、昼13時までの間で、1時間程度のオンライン授業を予定しております。
対象の生徒さんは、新小6、新小5年生ですが、新小4の生徒さんも可能です。
ただし、朝10時から昼13時という時間帯は、生徒さんは学校に行かれてますので、実際の授業は、お母様かお父様にすることになります。
ズームの授業は、録画が可能ですので、その録画を後でお子様に見せられてもいいですし、ズーム授業を受けられたお母様、お父様が、お子様に解き方を教えられてもいいと思います。
当ブログは、「パパママ算数教室」と名乗っている通り、基本的には、お子様の中学受験の算数を教えてあげたい、手伝ってあげたいお父様、お母様向けのブログですので、ズーム授業も親御さんが受ける前提で、このような時間帯にしております。
また、私自身が、ズームを使用するのも初めての上、オンライン授業や親御さん相手の授業も初めての手探り状態でのスタートとなりますので、最初のうちは無料で行います。
3月下旬から4月上旬にかけて、春季講習で出来ない期間もありますが、その間を除いて1ヶ月間ぐらいは無料でオンライン授業をやりたいと思いますので、3月1日から4月15日ぐらいまでは無料にしたいと思います。
また、時間帯も朝10時からとなっていますが、需要があれば、朝9時ぐらいからスタートしてもいいですし、授業も1時間程度としていますが、40分程度でも、1時間以上でも、ご要望により、柔軟に対応したいと思います。
というように、私自身も初めてのことなので、実際に無料のオンライン授業を経験しながら、良い形にしていこうと思っていますので、ご興味がある方は、お気軽にぜひメールをしていただきたいと思います!
読者のみなさま、よろしくお願いいたします!( ^_^)/