
いよいよ明日2月1日は、東京、神奈川の私立中入試が始まり、有名難関私立中学受験生の勝負の時がきますね!
首都圏の受験生のみなさん、明日は志望校合格目指して、頑張ってくださいね!!(^o^)/
一方、私が暮らす九州では、今年の中学受験はほぼ終了し、来年の中学入試に向け、小5の生徒の受験準備に移行しています。
そこで、改めて、現時点での志望校を書いてもらっているのですが、自分の志望校なのに、学校名をひらがなで書いたり、漢字を間違えて書くなど、先が思いやられるような生徒もいます・・(;^_^A
確かに難しい漢字やまだ未習の漢字のついた学校もありますが、小学3年生か4年生までに習ってるはずの漢字を間違えたり、ひらがなで書いたり・・
まあ、自分自身が合格したいと強く希望しているというよりも、親に勧められて、なんとなく受験するという感じの生徒は多いですから、その学校の漢字もあまり意識したことがないという感じですね・・(;^_^A
逆に、九州だと、ラ・サール中ならば、カタカナオンリーなので簡単に書けますが、簡単にラ・サールを志望校に挙げる生徒はそうそういませんね・・(;^_^A
それでは、今日は、名前に「難しい」が含まれている上に、入試問題も、合格することも難しいという名実共に超難関校「灘中学校」の今年の入試問題4⃣5⃣6⃣を解いていきましょう!
2021年 灘中 4⃣ 旅人算、相当算

正方形BADCを下図のように直線に直して考えてみましょう。
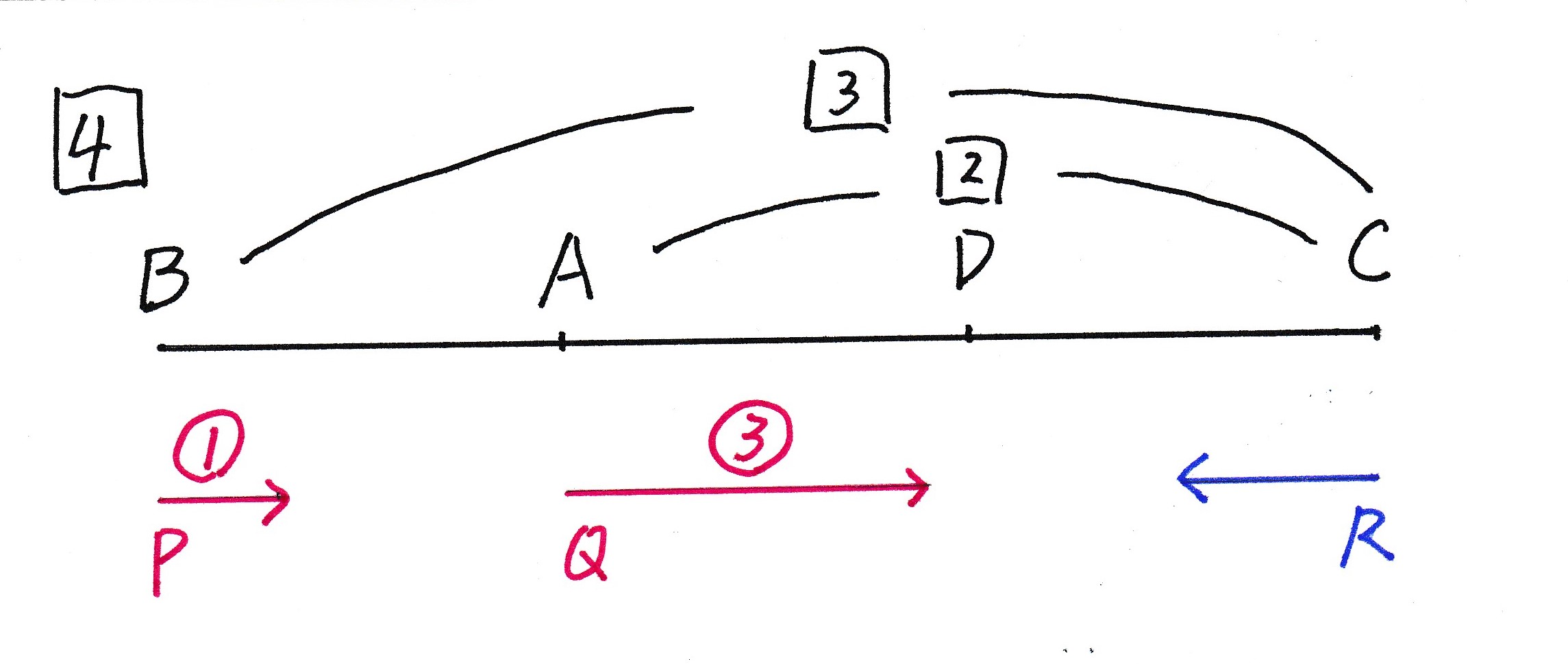
正方形の一辺の長さを1⃣とすると、BC=3⃣、AC=2⃣となる。
また、問題文より、Pの動く速さを①とすると、Qの動く速さは③となる。 Rの速さはRとする。
そこで、PとR、QとRが出会うのにかかる時間を旅人算で求める。

問題文より、PとRが出会う時間は、QとRが出会う時間の2倍なので、

線分を用いて、Rの値を求める。


2021年 灘中 5⃣ 整数問題、周期問題

これは単純そうですが、計算の数が多くなるので、時間がかかります。
そこで、余りのパターンを見つけることから始めます。
Aは二桁の数ですが、余りのパターンを見つける必要があるので、一桁の計算も必要となります。
1×1=1 1÷15=0・・1
2×2=4 4÷15=0・・4
3×3=9 9÷15=0・・9
4×4=16 16÷15=1・・1
5×5=25 25÷15=1・・10
6×6=36 36÷15=2・・6
7×7=49 49÷15=3・・4
8×8=64 64÷15=4・・4
9×9=81 81÷15=5・・6
10×10=100 100÷15=6・・10
11×11=121 121÷15=8・・1
12×12=144 144÷15=9・・9
13×13=169 169÷15=11・・4
14×14=196 196÷15=13・・1
15×15=225 225÷15=15 あまり0
16×16=256 256÷15=17・・1
17×17=289 289÷15=19・・4
・
・
と求めていくと、余りは、
{1,4,9,1,10,6,4,4,6,10,1,9,4,1,0}
と、15個ずつの周期で繰り返される。 その中に、余りが1になるのは、4個ある。
よって、Aが1から99だとすると、この15個ずつのセットが、
99÷15=6・・9
6セットできて、9個余る。
よって、6セットの中に含まれる余り1は、
4個×6=24個
また、余った9個の数字(A=91~99)の余りは、
1,4,9,1,10,6,4,4,6
なので、余り1は2個含まれる。
一方、Aは二桁の整数だが、6セットの中には、A=1~9の一桁の整数も含まれている。
このA=1~9の一桁の数字の余りも、
1,4,9,1,10,6,4,4,6
で、余り1は2個含まれるから、これは除かなければならない。
よって、A×Aを15で割って、余りが1になる二桁の整数Aは、
24+2ー2 = 24個
2021年 灘中 6⃣ 整数問題、約数


②を解くにあたり、まずは上の約分の仕方を工夫してやり直してみましょう。
分母にあたる6の約数は、それぞれ2倍された数字が分子の積に含まれている。
よって、下の分数のように、分母の数字を2倍した数字でそれぞれ約分すると、分母の約数の数だけ、2をかけることになる。

よって、②の式の値192を素因数分解してみると、下図のように、
192 = 1×3×2×2×2×2×2×2
となり、2が6回かけてあるので、分母Cの約数の個数は6個ということになる。

さらに、分子の〔2×C〕の約数に3が含まれているので、分母〔C〕の約数にも3が含まれることになる。
*約数に3を含むということは、その数は3の倍数であるから、〔2×C〕は6の倍数ということになる。
〔2×C〕=6 の場合 〔C〕=3
〔2×C〕=12 の場合 〔C〕=6
〔2×C〕=18 の場合 〔C〕=9
〔2×C〕=24 の場合 〔C〕=12
と、〔2×C〕が6の倍数の場合、〔C〕は3の倍数となるので、〔C〕の約数にも3が含まれることになる。
そこで、Cは約数を6個持つ3の倍数であるので、3の倍数の約数を数えてみると、
3の約数 (1、3)の2個
6の約数 (1、2、3、6)の4個
9の約数 (1、3、9)の3個
12の約数 (1、2、3、4、6、12)の6個
よって、C=12
今日のまとめ
今日の問題では、5⃣の余りの問題が大変でしたね・・
周期の問題は、5,6個で1セットということはよくありますが、今日の問題は15個で1セットなので、途中であきらめる生徒も多いのではないでしょうか?(;^_^A
一方、4⃣は比較的解きやすい問題だと思いますし、6⃣も②は適当に数字を入れてみたら解けたという生徒もいるかもしれませんが、解説のように、理論的に解けると、式の値が大きくなっても解けるようになりますので、頑張って理解するようにしてくださいね!( ^_^)/







